PERSPECTIVES on Language and Literacy
A Quarterly Publication of The International Dyslexia Association Volume 37, No. 2
Mathematical Difficulties in School Age Children
http://www.interdys.org
I have inserted my own annotations in green.

by Daniel B. Berch
Some school-age children struggle with mathematics, routinely experiencing difficulty in learning or remembering basic arithmetic facts and carrying out even the seemingly most elementary numerical operations (Berch & Mazzocco, 2007). Such difficulties are compounded when students are expected to build upon these basic skills as they are introduced to increasingly abstract, mathematical content domains. Consider a letter published in the Washington Post written by a seventh-grade teacher not that long ago:
Many of the seventh graders I teach
have a poor sense of numbers. They don’t understand
that adding two numbers results in a larger number,
that multiplication is repeated addition, that 5
× 6 is larger than 5 × 4 or that one
quarter is smaller than one half. This lack of basic
math facts detracts from their ability to focus on
the more abstract operations required in math at a
higher level” (Susan B. Sheridan, Washington
Post, December 27, 2004).
Notice that she isn't a special ed teacher.
Many plain, ordinary students are in 7th
grade with this level of confusion. No wonder they
don't understand algebra!
What are the key factors contributing to this state of affairs? Is the problem due primarily to poor instruction, or is there something inherently difficult about learning even basic arithmetic because of the ways in which the developing child’s mind works? Have we been able to trace the origins of extremely low math performance that would warrant the diagnosis of a mathematical learning disability? And do effective remedial approaches exist for improving the mathematics achievement of such children?
As it turns out, definitive answers to these weighty questions still elude us. Nonetheless, progress is being made on a number of fronts, especially in the study of the fundamental cognitive processes that underlie mathematical thinking in general and those that are crucial for achieving proficiency in carrying out arithmetic calculations in particular. In this article, I will review what we have learned about the contributions of an especially important factor known as “working memory,” along with the difficulties that can arise for students who exhibit weaknesses if not outright deficits in the full complement of skills comprising this construct.
Introduction to the Concept of Working Memory
Precisely what do we mean when invoking the concept of working memory? As this cognitive construct actually encompasses several mental operations, definitions of working memory tend to vary considerably (Dowker, 2005; Shah & Miyake, 1999). Furthermore, although this concept seems comparatively straightforward at one level, it turns out to be much more complicated at another. Such a view is shared by many, including Susan Pickering, a leading researcher in this field who acknowledged that “The concept of working memory is both reassuringly simple and frustratingly complex” (2006, p. xvi).
As a consequence, it may prove instructive to present an example of how working memory can influence arithmetic problem solving before providing a definition. To begin with, consider the following quote taken from Lewis Carroll’s Through the Looking-Glass (1871) which Kaufman (2010) describes as “A working memory lapse in Wonderland”
(p. 153): “‘And you do addition?’ the White Queen asked. ‘What’s one and one and one and one and one and one and one and one and one and one?’ ‘I don’t know,’ said Alice, ‘I lost count.’”
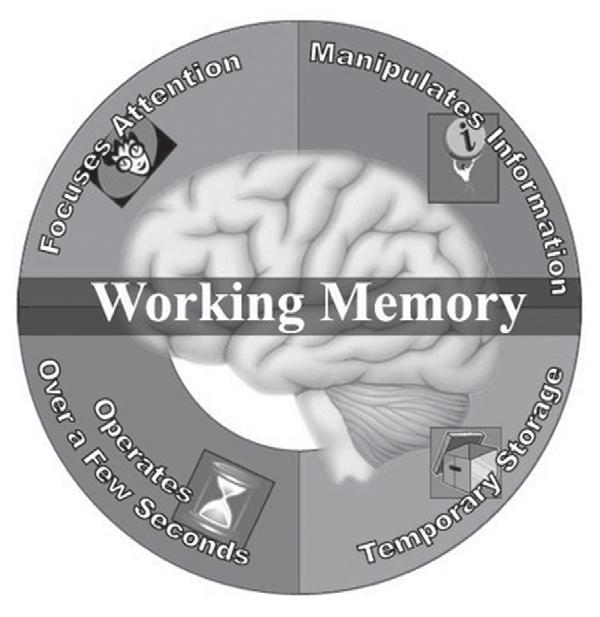
Components of the working memory system. Reprinted from Working-Memory-and-Education – Introduction to Working Memory (WM), D. B. Berch, Retrieved November 17, 2010, from http://working-memory-and-education.wikispaces.com/ Introduction+to+Working+Memory+(WM). Copyright 2009 by Carren Tatton. Reprinted with permission.
Although it is doubtful that Alice’s failure to solve this problem is attributable to a mathematical learning disability, the example illustrates nicely some of the key components of working memory depicted in Figure 1. That is, in order not to lose count when attempting to solve such a problem, an individual would have to: a) focus attention on each new addend as it is presented, b) manipulate the information by mentally adding the “ones,” and at the same time, c) selectively maintain some of the information (in this case, the most recent prior sum)in temporary mental storage, and d) complete all of these tasks within the span of a few seconds. In other words, working memory is probably best defined as a limited capacity system responsible for temporarily storing, maintaining, and mentally manipulating information over brief time periods to serve other ongoing cognitive activities and operations. In essence, it constitutes the mind’s workspace.
Getting back
to the White Queen’s
arithmetic problem,
while adding single
digits should be
comparatively easy for
most typically achieving
seven-and-a-half-year-olds
(Alice’s age), it is
evident from this
example that one can
excessively tax working
memory by requiring a
learner to
simultaneously attend,
store, and mentally
process a rather large
amount of information
(albeit elementary in
some sense) within a
relatively short period
of time. As Susan
Gathercole, another
leading researcher in
this field has pointed
out, overloading this
fragile mental workspace
can lead to “complete
and catastrophic loss of
information from working
memory” (Gathercole,
2008, p. 382).
Complete
and catastrophic loss
-- sadly, that's what
happens all too often
to math students.
. . . working memory is probably best defined as a limited capacity system responsible for temporarily storing, maintaining, and mentally manipulating information over brief time periods to serve other ongoing cognitive activities and operations.
Obviously, no
teacher would deliberately
choose to overload
his or her students’ working
memory capacity. Nevertheless,
mathematical information can
sometimes be presented in a
manner (e.g., orally or in
textbooks) that inadvertently
strains the processing
capacity of students.
Practitioners can learn to
readily avoid these situations
if they are furnished with
some basic information about
the nature of working memory,
its limitations, and the ways
in which students can differ
with respect to its
constituent skills.
Accordingly, the purpose of
this article is to provide
non-specialists with a
succinct overview of the
latest research on this topic,
which I have organized in a
way that I hope will shed
light on some of the most
important questions pertaining
to the role of working memory
in learning school
mathematics, including: What
are the ways in which working
memory’s component skills can
be measured? How do
limitations in working memory
contribute to the development
of mathematical learning
difficulties and disabilities?
And finally, what kinds of
instructional interventions or
remedial approaches are
available for mitigating the
detrimental effects of working
memory limitations on
mathematics achievement?
So
diplomatically
stated! I disagree
about being able to "readily
avoid" these situations given
the current state of math
instruction. On the other
hand, there are times when,
really, the main issue is
working memory. I'm
curious about the instructional
aspect -- will motor memory
stuff be included?
How Are Working Memory Skills Measured?
Children’s working memory skills are customarily assessed with a variety of what are referred to as “simple” and “complex” span tasks. Simple span tasks are used to measure the short-term storage capacity of two types of domain-specific representations: verbal and visuospatial. To appraise the former, a reading or listening span measure is usually employed that entails the recall of word or number sequences; when assessing the latter, either the recall of random block-tapping sequences or randomly filled cells in a visual matrix or grid is typically required.
In contrast, complex span tasks gauge domain-general, central attentional resources by imposing substantial demands both on mental storage and processing (Holmes, Gathercole, & Dunning, 2010). As I have described elsewhere (Berch, 2008), a particularly representative example of such a measure is the Backward Digit Span task in which a random string of number words is spoken by the examiner (e.g., saying “seven, two, five, eight . . .”), and the child must try to repeat the sequence in reverse order. Note that rather than simply having to recall the numbers in the same forward order (which is considered a measure of the short-term, verbal storage component per se), the backward span task requires that the child both store and maintain the forward order (i.e., verbal component) of the number words while simultaneously having to mentally manipulate this information to accurately recite the original sequence in the opposite order. It is this dynamic coordination and control of attention combined with the storing and manipulation of information in support of ongoing cognitive activities that I characterized earlier as being the sine qua non of working memory.
To carry out a comprehensive assessment of children’s working memory capacities, most researchers currently make use of one of two standardized batteries—the Working Memory Test Battery for Children (Pickering & Gathercole, 2001) or the Automated Working Memory Assessment (Alloway, 2007). As Holmes and her colleagues (2010) describe, each of these is comprised of several subtests, affording multiple assessments of different facets of working memory (e.g., central attentional resources as well as verbal and visuospatial short-term storage components). Additionally, these batteries permit the identification of children with poor working memory for their chronological age, based on existing norms.
Another technique for identifying children with poor working memory is derived from ratings provided by a child’s teacher, a prominent example being the Working Memory Rating Scale (Alloway, Gathercole, & Kirkwood, 2008). This measure consists of approximately 20 statements of problem behaviors such as “She lost her place in a task with multiple steps” and “The child raised his hand but when called upon, he had forgotten his response.” Teachers rate how typical each of these behaviors is of a given child using a four-point scale. Although this technique affords a fast and efficient method for initial identification of working memory problems in a school setting (Holmes et al., 2010), it is probably best used as one component of a comprehensive evaluation by the school psychologist. Furthermore, if need be, teachers can choose to make supplementary, informal observations for guiding adjustments to their instructional approaches with particular children.
How Do Working Memory Limitations Contribute to Mathematical Learning Difficulties?
As noted earlier, measures of working memory are usually designed to assess one or more of three presumed subsystems comprising what is known as a multicomponent model: a domain-general, limited capacity central executive that governs the storage and temporary maintenance of information in two domain-specific representational subsystems—the phonological loop and visuospatial sketchpad—by means of attentional control (Baddeley, 1990, 1996; Baddeley & Hitch, 1974). To date, the vast majority of investigations aimed at determining particular relationships between various working memory skills and mathematics learning or performance have been based on this model.
Such
relationships have been studied in
children ranging from preschool age to
adolescence, and for math skills extending
from the very basic (e.g., numerical
transcoding—writing an Arabic numeral in
response to hearing a number word,
counting, numerical magnitude comparison,
and single-digit addition and subtraction)
to more complex mathematical operations
and content domains, such as multidigit
arithmetic, rational numbers, and
algebraic word problem solving.
Furthermore, according to Raghubar,
Barnes, and Hecht (2010), numerous other
factors may influence and therefore
complicate the interpretation of findings
pertaining to the relations between
working memory and math performance,
including but not limited to skill level,
language of instruction, how math problems
are presented, the type of math skill at
issue, whether that skill is just being
acquired or has already been mastered, the
type of working memory task administered,
and the kinds of strategies that
different-aged children operating at
diverse skill levels may employ for a
given task.
Comment
from me: Emotional state isn't
mentioned -- but anxiety wreaks havoc on
working memory!
Consistent with
this perspective, Geary and his colleagues
(Meyer, Salimpoor, Wu, Geary, & Menon
2010) highlighted the importance of their
findings that the contributions of
particular components of working memory to
individual differences in mathematics
achievement can vary with grade level or
the type of math content being assessed.
More specifically, these researchers
showed that the central executive and
phonological loop play a more important
role in facilitating mathematics
performance for second graders, while the
visuospatial sketchpad does so for third
graders. Furthermore, they provide a
compelling argument that this grade-level
difference is attributable to instruction
and practice rather than a developmental
change in working memory capacity.
Fascinating!
What happens
later?
Is this what I
see when I
watch students
imitate what a
problem looks
like instead
of discerning
what it means?
All this being
said, earlier reviews of research on this
topic (DeStefano & LeFevre, 2004;
Swanson & Jerman, 2006) along with
more recent ones (Geary, 2010; Raghubar et
al., 2010) have yielded reasonably clear
evidence of a generally strong association
between working memory capacity and
mathematics performance. *Indeed, even the
leading proponent of the view that the
development of mathematical learning
disabilities is attributable to a deficit
in a domain-specific, inherited system for
coding the number of objects in a set has
recently acknowledged that the
domain-general, central executive
functions of working memory are at the
very least associated (i.e., correlated)
with arithmetic learning and performance
(Butterworth, 2010). What is the nature of
this relationship? As Geary (2010)
concludes after reviewing the findings,
the greater the capacity of the central
executive, the better the performance both
on cognitive mathematics tasks and math
achievement tests (Bull, Espy, &
Wiebe, 2008; Mazzocco & Kover, 2007;
Passolunghi, Vercelloni, & Schadee,
2007). Furthermore, Geary notes that the
phonological loop seems to be important
for verbalizing numbers, as in counting
(Krajewski & Schneider, 2009) and in
solving math word problems (Swanson &
Sachse-Lee, 2001).
*Is this
because "performance" is measured in
how well students perform symbolic
procedures? As in, Math is abotu
memorizing symbol manipulation, so
the kiddo who actually is
mathematically gifted is going to
perform poorly because that's not
how we teach it?
. . . factors (that) may influence . . . the relations between working memory and math performance (include) skill level, language of instruction, how math problems are presented, the type of math skill at issue, whether that skill is just being acquired or has already been mastered, the type of working memory task administered, and the kinds of strategies that different-aged children operating at diverse skill levels may employ for a given task.
Although studies have also shown that children with either math learning difficulties or disabilities exhibit deficits in all three working memory subsystems, Geary (2010) concludes that impairment in their central executive appears to be particularly troublesome (Bull, Johnston, & Roy, 1999; Swanson, 1993). However, Geary also observes that the interpretation of these findings is complicated by the fact that at least three purported subcomponents of the central executive (i.e., inhibition, updating, and attention shifting) have been found to influence math learning in different ways (Bull & Scerif, 2001; Murphy, Mazzocco, Hanich, & Early, 2007; Passolunghi, Cornoldi, & De Liberto, 1999; Passolunghi & Siegel, 2004).
In summing up what researchers have learned about associations between working memory and math learning disabilities, Geary (2010) affirms that: “At this point, we can conclude that children with MLD have pervasive deficits across all of the working memory systems that have been assessed, but our understanding of the relations between specific components of working memory and specific mathematical cognition deficits is in its infancy” (p. 62).
What Kinds of Interventions or Remedial Approaches Exist for Improving Working Memory?
In a review of techniques used to date for mitigating the difficulties encountered by children who have poor working memory, Holmes and her colleagues (2010) grouped these under three main approaches: 1) a classroom-based intervention that consists of encouraging teachers to adapt their instructional approaches in ways that minimize working memory loads; 2) training designed to teach children to make use of
Working Memory and Mathematics Learning continued from page 23
| TABLE 1. Principles of the Classroom-Based Working Memory Approach | |
|---|---|
| Principles | Further Information |
| Recognize working memory failures | Warning signs include recall, failure to follow instructions, place-keeping errors, and task abandonment |
| Monitor the child | Look out for warning signs, and ask the child |
| Evaluate working memory loads | Heavy loads caused by lengthy sequences, unfamiliar and meaningless content, and demanding mental processing activities |
| Reduce working memory loads | Reduce the amount of material to be remembered, increase the meaningfulness and familiarity of the material, simplify mental processing, and restructure complex tasks |
| Repeat important information | Repetition can be supplied by teachers or fellow pupils nominated as memory guides |
| Encourage use of memory aids | These include wall charts and posters, useful spellings, personalized dictionaries, cubes, counters, abaci, Unifix blocks, number lines, multiplication grids, calculators, memory cards, audio recorders, and computer software |
| Develop the child’s own strategies | These include asking for help, rehearsal, note-taking, use of long-term memory, and place-keeping and organizational strategies |
Note. Adapted from “Working memory in the classroom,” by S. E. Gathercole, 2008, The Psychologist, 21, 382–385. Copyright 2008 by The British Psychological Society. Adapted with permission.
memory
strategies for improving the efficiency
of working memory; and 3) training aimed
directly at improving working memory
through the use of an adaptive
computerized program that involves
repeated practice on working memory
tasks.
Again,
assuming it's a neurological deficit
would be, I believe, a mistake because
if you understand what's going on, you
don't *need* as much working memory.
The classroom-based intervention
is founded on a set of seven principles
that originated from both classroom
practice and cognitive theory (Gathercole,
2008) and are summarized in Table 1.
Recently, a research team carried out an
evaluation over a one-year period of two
forms of this intervention aimed at
primary school children with poor working
memory (Elliott, Gathercole, Alloway,
Holmes, & Kirkwood, 2010). Although
there was no evidence that the
intervention programs directly improved
either working memory or academic
performance, the extent to which teachers
implemented these seven principles was
predictive of their students’ mathematical
(and literacy) skills. Furthermore,
teachers were reportedly very pleased
about the ways in which the intervention
had improved their own understanding and
practice (which exemplifies the kind of
mathematics knowledge enhancement that Dr.
Murphy and her colleagues (this issue)
promote for all teachers). Additional
studies exploring how best to implement
this kind of intervention are clearly
warranted if we are to determine the
optimal ways for practitioners to enhance
children’s mathematics achievement through
the strengthening of working memory
skills.
TEachers
had their own
understanding
improved...
there's rather
an important
key.
With respect to the strategy training approach, the kinds of memory strategies children have been taught to use include repetitively rehearsing information, generating sentences from words or making up stories based on them, or creating visual images of the information (Holmes et al., 2010). Strategy training incorporating all of these techniques was recently administered to children ranging in age from five to eight years old in two sessions per week over a six-to-eight-week period using a computerized adventure game (St. Clair-Thompson, Stevens, Hunt, & Bolder, 2010). Although training significantly enhanced both verbal short-term memory and working memory, there were no gains in visuospatial short-term memory. More relevant to the focus of this article, performance on a mental arithmetic task improved significantly. Furthermore, all of these gains were evidenced by children with poor working memory as well as those with average working memory. Nevertheless, no significant changes emerged on standardized assessments of arithmetic or other mathematical domains either immediately following training or five months afterward.
Yo. this is probably more imporant
than we think. *Everybody*
improved, not just the people with
poor working memory ... and nobody
actually did better on math tests.
Hmmm....
. . . the extent to which teachers implemented these seven principles (of working memory intervention) was predictive of their students’ mathematical (and literacy) skills.
Finally,
according to Holmes and her colleagues
(2010), the most impressive gains in
working memory obtained thus far have
resulted from a direct training program
developed originally for use with
children with attention deficit
hyperactivity disorder (ADHD; Klingberg
et al., 2005; Klingberg, Forssberg,
& Westerberg, 2002). Children
undergoing this intensive training
regimen participate in a variety of
computerized tasks designed to
repeatedly tax their working memory
capacity (i.e., requiring simultaneous
storage and manipulation of information)
to the greatest extent possible without
exceeding a level they can still manage
effectively. This is achieved by
matching the difficulty of each
successive task to a child’s current
memory span on a trial-by-trial basis.
Holmes, Gathercole, and Dunning (2009)
administered this so-called adaptive
training program to 9- and 10-year-olds
with poor working memory skills in 20
training sessions, each 35 minutes long,
over a period of five to seven weeks.
Not only did the children exhibit
sizeable improvements in verbal and
visuospatial working memory, but six
months later these gains had still not
declined. And even though no gains were
found on a standardized mathematics
reasoning test immediately after
training, a small but significant
improvement emerged on the six-month
follow-up assessment.
Fascinating
-- for the computerized training,
having the good working memory had 'em
doing better six months later. I
bet this one would have worked for the
normal kiddos, too, perhaps???
In sum, although these three types of interventions have been shown to improve working memory skills, evidence of their impact on academic performance in general and on mathematics abilities in particular is as yet rather limited (Holmes et al., 2010). However, it is our hope that continued study of ways to enhance such outcomes will yield stronger proof regarding whether such training can transfer to students’ mathematics performance.
One final investigation is worth describing here, primarily because even though it was a cognitive laboratory study, it has important implications for improving classroom instruction. Briefly, this investigation revealed that although the working memory capacity of seven-year-olds is smaller than that of older children and adults, their attentional processes are just as efficient—so long as their smaller working memory capacity is not exceeded (Cowan, Morey, AuBuchon, Zwilling, & Gilchrist (2010). However, when their working memory is overloaded, attentional efficiency declines, suggesting that interventions aimed at enhancing working memory will in turn improve attentional efficiency. As these researchers put it, “In general, children’s attention to relevant information can be improved by minimizing irrelevant objects or information cluttering working memory” (p. 131).
Conclusions
Taken together, the research reviewed in this article shows that we are making significant progress toward achieving a more complete understanding of the nature of working memory, its typical course of development, and the best methods for assessing its various features. We have also made important advances in discerning how working memory limitations and impairments can hinder the attainment of proficiency in mathematics, and we have just begun to explore the most promising strategies that can be implemented to enhance the working memory skills most relevant for improving students’ mathematical learning and performance. Finally, I hope that the information provided here will be of some use to those of you who teach in identifying working memory limitations in your students, modifying the instructional environment to minimize extraneous or distracting information that might interfere with efficient selective attention, and designing strategies for enhancing your students’ working memory skills.
References
Alloway, T. P. (2007). Automated working memory assessment. Oxford, UK: Pearson Assessment.
Alloway, T. P., Gathercole, S. E., & Kirkwood, H. (2008). Working Memory Rating Scale. Oxford, UK: Pearson Assessment.
Baddeley, A. D. (1990). Human memory: Theory and practice. Hove, UK: Lawrence Erlbaum Associates.
Baddeley, A. D. (1996). Exploring the central executive. Quarterly Journal of Experimental Psychology, 49A, 5–28.
Baddeley, A. D., & Hitch, G. J. (1974). Working memory. In G. H. Bower (Ed.), The psychology of learning and motivation, Vol. 8 (pp. 47–89). New York: Academic Press.
Berch, D. B. (2008). Working memory and mathematical cognitive development: Limitations of limited-capacity resource models. Developmental Neuropsychology, 33, 427−446.
Berch, D. B., & Mazzocco, M. M. M. (Eds.). (2007). Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. Baltimore: Paul H. Brookes.
Bull, R., Espy, K. A., & Wiebe, S. A. (2008). Short-term memory, working memory, and executive functions in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology, 33, 205–228.
Bull, R., Johnston, R. S., & Roy, J. A. (1999). Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: Views from cognition and developmental neuropsychology. Developmental Neuropsychology, 15, 421–442.
Bull, R., & Scerif, G. (2001). Executive functioning as a predictor of children’s mathematical abilities: Inhibition, switching, and working memory. Developmental Neuropsychology, 19, 273–293.
Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends in Cognitive Sciences, 14, 534–541.
Cowan, N., Morey, C. C., AuBuchon, A. M., Zwilling, C. E., & Gilchrist, A. L. (2010). Seven-year-olds allocate attention like adults unless working memory is overloaded. Developmental Science, 13, 120–133.
DeStefano, D., & LeFevre, J.-A. (2004). The role of working memory in mental arithmetic. European Journal of Cognitive Psychology, 16, 353–386.
Dowker, A. (2005). Individual differences in arithmetic: Implications for psychology, neuroscience and education. New York: Psychology Press.
Elliott, J. G., Gathercole, S. E., Alloway, T. P., Holmes, J., & Kirkwood, H. (2010). An evaluation of a classroom-based intervention to help overcome working memory difficulties and improve long-term academic achievement. Journal of Cognitive Education and Psychology, 9, 227–250.
Gathercole, S. E. (2008). Working memory in the classroom. The Psychologist, 21, 382–385.
Geary, D. C. (2010). Mathematical learning disabilities. In J. Holmes (Ed.), Advances in Child Development and Behavior, Vol. 39 (pp. 45–77). Burlington: Academic Press.
Holmes, J., Gathercole, S. E., & Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children. Developmental Science, 12, F9–F15.
Holmes, J., Gathercole, S. E., & Dunning, D. L. (2010). Poor working memory: Impact and interventions. In J. Holmes (Ed.), Advances in Child Development and Behavior, Vol. 39 (pp. 1–43). Burlington: Academic Press.
Kaufman, C. (2010). Executive function in the classroom: Practical strategies for improving performance and enhancing skills for all students. Baltimore: Paul H. Brookes.
Klingberg, T., Fernell, E., Olesen, P. J., Johnson, M., Gustafsson, P., Dahlstrom, K. et al. (2005). Computerised training of working memory in children with ADHD— A randomised controlled trial. Journal of the American Academy of Child and Adolescent Psychiatry, 44, 177–186.
Klingberg, T., Forssberg, H., & Westerberg, H. (2002). Increased brain activity in frontal and parietal cortex underlies the development of visuospatial working memory capacity during childhood. Journal of Cognitive Neuroscience, 14, 1–10.
Krajewski, K., & Schneider, W. (2009). Exploring the impact of phonological awareness, visual–spatial working memory, and preschool quantity–number competencies on mathematics achievement in elementary school: Findings from a 3-year longitudinal study. Journal of Experimental Child Psychology, 103, 516–531.
Mazzocco, M. M. M., & Kover, S. T. (2007). A longitudinal assessment of executive function skills and their association with math performance. Child Neuropsychology, 13, 18–45.
Meyer, M. L., Salimpoor, V. N., Wu, S. S., Geary, D. C., & Menon V. (2010). Differential contribution of specific working memory components to mathematical skills in 2nd and 3rd graders. Learning and Individual Differences, 20, 101–109.
Murphy, M. M., Mazzocco, M. M. M., Hanich, L. B., & Early, M. C. (2007). Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. Journal of Learning Disabilities, 40, 458–478.
Passolunghi, M. C., Cornoldi, C., & De Liberto, S. (1999). Working memory and intrusions of irrelevant information in a group of specific poor problem solvers. Memory & Cognition, 27, 779–790.
Passolunghi, M. C., & Siegel, L. S. (2004). Working memory and access to numerical information in children with disability in mathematics. Journal of Experimental Child Psychology, 88, 348–367.
Passolunghi, M. C., Vercelloni, B., & Schadee, H. (2007). The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cognitive Development, 22, 165–184.
Pickering, S. J. (Ed.). (2006). Working memory and education. London: Elsevier.
Pickering, S., & Gathercole, S. (2001). Working memory test battery for children (WMTB-C). London: The Psychological Corporation.
Raghubar, K. P., Barnes, M. A., & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences, 20, 110–122.
Shah, P., & Miyake, A. (1999). Models of working memory: An introduction. In A. Miyake & P. Shah (Eds.), Models of working memory: Mechanisms of active maintenance and executive control (pp. 1–27). New York: Cambridge University Press.
St. Clair-Thompson, H. L., Stevens, R., Hunt, A., & Bolder, E. (2010). Improving children’s working memory and classroom performance. Educational Psychology, 30, 203–220.
Swanson, H. L. (1993). Working memory in learning disability subgroups. Journal of Experimental Child Psychology, 56, 87–114.
Swanson, H. L., & Jerman, O. (2006). Math Disabilities: A selective meta-analysis of the literature. Review of Educational Research, 76, 249–274.
Swanson, H. L., & Sachse-Lee, C. (2001). Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important. Journal of Experimental Child Psychology, 79, 294–321.
Daniel B. Berch, Ph.D., is a Professor of Educational Psychology and Applied Developmental Science at the University of Virginia’s Curry School of Education. He has authored assorted articles and book chapters on children’s numerical cognition and mathematical learning disabilities, and is senior editor of the book (co-edited by Dr. Michèle Mazzocco), Why Is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities. Dr. Berch served on the National Mathematics Advisory Panel commissioned by President George W. Bush and is a member of the National Center for Learning Disabilities Professional Advisory Board.